예전 카카오코드 예선 문제를 풀어보다가 DFS 알고리즘을 사용하게 되어 다시 한번 복습해보게 되었습니다.
문제: https://programmers.co.kr/learn/courses/30/lessons/1829
비슷한 유형의 문제들이 많이 있는데 대부분은 DFS를 사용하면 풀 수 있습니다. 해당 문제를 DFS로 풀 경우 시간복잡도는 O(m*n)이 됩니다. m과 n은 가로와 세로의 크기입니다. DFS와 BFS는 기본적으로 모든 노드를 한 번씩 거쳐 가기 때문에 Brute Force의 일종으로 볼 수 있는 방법입니다. DFS와 BFS의 원리에 대해서 알아보겠습니다.
Depth-First Search
깊이 우선 탐색은 시작점에서 한 쪽으로 가장 깊은 방향을 우선 탐색하는 방법입니다. 한쪽 방향으로 끝장을 본 후, 다른 방향을 새로 탐색하는 방법입니다. 미로 풀이에 쓰기 위해 처음 고안된 방법으로 한쪽 벽을 짚고 가다 보면 언젠가 출구가 나오는 방법을 수학적 알고리즘으로 표현한 것입니다. 시간 복잡도는 일반적으로 O(|V| + |E|)로 나타냅니다. V는 노드의 개수, E는 간선의 개수입니다. 공간 복잡도는 O(|V|)입니다.
의사 코드
procedure DFS(G,v):
label v as discovered
for all directed edges from v to w that are in G.adjacentEdges(v) do
if vertex w is not labeled as discovered then
recursively call DFS(G,w)
재귀적 방법
procedure DFS-iterative(G,v):
let S be a stack
S.push(v)
while S is not empty
v = S.pop()
if v is not labeled as discovered:
label v as discovered
for all edges from v to w in G.adjacentEdges(v) do
S.push(w)
Stack을 이용한 방법
하지만 의사 코드는 이해가 쉽지 않습니다. 우리가 매일 보는 실제 코드랑 다르게 논리적인 로직만 있기 때문입니다. 최대한 이해가 쉽도록 의사 코드를 그대로 JAVA를 이용해 구현해 보겠습니다.
재귀를 이용한 구현
class Graph {
private ArrayList<Integer>[] graph;
private boolean[] visited;
public Graph(int size){
graph = new ArrayList[size + 1];
for (int i = 0; i < size + 1; i++)
graph[i] = new ArrayList<Integer>();
visited = new boolean[size + 1];
}
public void addEdge(int m, int n) {
graph[m].add(n);
graph[n].add(m);
}
public List<Integer> adjacentEdges(int node) {
return graph[node];
}
public static void DFS(Graph G, int v) {
// label v as discovered
G.visited[v] = true;
System.out.print(v + " ");
// for all directed edges from v to w that are in G.adjacentEdges(v) do
for(int w: G.adjacentEdges(v)) {
// if vertex w is not labeled as discovered then
if (!G.visited[w])
// recursively call DFS(G, w)
DFS(G, w);
}
}
}
의사 코드가 JAVA 코드에 일대일 대응이 되도록 구현했습니다. 실제 코드로 보니 이해가 더 쉽습니다. int형 정수가 그래프의 각 노드에 해당하는 번호라고 볼 수 있고, 그래프는 목록의 행렬로 구현했습니다. 그래프를 구현하는 방법은 이차원 행렬 혹은 목록이 있는데, 각각 장단점이 있습니다. 이차원 행렬은 공간복잡도가 m*m으로 늘어나지만 간선에 가중치를 줄 수 있고, 목록은 단순한 연결 상태만을 표현하지만 공간복잡도가 실제 간선의 연결상태에 따라 달라집니다.
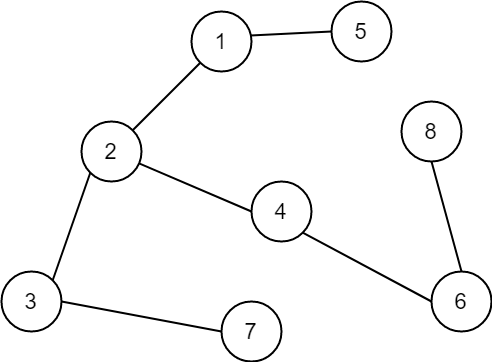
숫자는 노드의 번호로 탐색 순서가 아닙니다.
실제로 위 트리를 작성한 코드를 이용하여 DFS를 수행해보겠습니다.
public class Main {
public static void main(String[] args) {
int[][] edges = new int[][]{
{1, 2}, {1, 5}, {2, 3},
{3, 7}, {2, 4}, {4, 6},
{6, 8}};
Graph graph = new Graph(9);
graph.addEdge(edges);
Graph.DFS(graph, 1);
}
}
1 2 3 7 4 6 8 5
Stack을 이용한 구현
재귀적인 방법이 아닌 스택 자료 구조를 이용해서 DFS를 구현할 수 있습니다. 스택을 사용하는 이유는 스택의 특징인 FILO가 탐색 방식에 어울리기 때문입니다.
class Graph {
private ArrayList<Integer>[] graph;
private boolean[] visited;
public Graph(int size) {
graph = new ArrayList[size + 1];
for (int i = 0; i < size + 1; i++)
graph[i] = new ArrayList<Integer>();
visited = new boolean[size + 1];
}
public void addEdge(int m, int n) {
graph[m].add(n);
graph[n].add(m);
}
public void addEdge(int[][] edges) {
for (int[] edge : edges)
addEdge(edge[0], edge[1]);
}
public List<Integer> adjacentEdges(int node) {
return graph[node];
}
public static void DFS_iterative(Graph G, int v) {
// let S be a stack
Stack<Integer> S = new Stack();
// S.push(v)
S.push(v);
// while S is not empty
while (!S.empty()) {
// v = S.pop()
v = S.pop();
// if v is not labeled as discovered:
if (!G.visited[v]) {
// label v as discovered
G.visited[v] = true;
System.out.print(v + " ");
// for all edges from v to w in G.adjacentEdges(v) do
for (int w = G.adjacentEdges(v).size(); w > 0; w--) {
// S.push(w)
S.push(G.adjacentEdges(v).get(w - 1));
}
}
}
}
}
나머지 코드는 동일하고 스택을 이용한 DFS 함수만 추가했습니다.
동일하게 테스트해보겠습니다.
public class Main {
public static void main(String[] args) {
int[][] edges = new int[][]{
{1, 2}, {1, 5}, {2, 3},
{3, 7}, {2, 4}, {4, 6},
{6, 8}};
Graph graph = new Graph(9);
graph.addEdge(edges);
Graph.DFS_iterative(graph, 1);
}
}
1 2 3 7 4 6 8 5
정렬되지 않은 목록을 사용했기 때문에 같은 순서를 얻기 위해 for문으로 push를 할 때 역순으로 수행했습니다. 실제로는 정렬 방식과 구현 방식에 따라 Ordering을 결정할 수 있습니다. 구현된 예제에서는 이 부분은 생략했습니다. 이처럼 스택 혹은 재귀를 사용해서 DFS를 동일하게 구현할 수 있습니다. 하지만 재귀를 이용해 구현할 경우 그래프의 깊이만큼 스택 프레임이 쌓이는 문제점이 있기 때문에 그래프의 깊이가 깊을 경우 스택(자료구조)를 사용하여 구현하는게 좋습니다.
Breadth-First Search
너비 우선 탐색은 시작점에서 가장 가까운 노드들을 탐색한 후 그 다음 깊이 레벨의 노드들을 탐색하는 방법입니다. BFS역시 미로의 출구를 찾을 수 있지만, 가까운 데부터 탐색하는 특성상 출구까지의 최단거리 해법을 찾는 데 유용합니다. 시간복잡도와 공간복잡도는 DFS와 동일합니다.
의사 코드
procedure BFS(G,start_v):
let Q be a queue
label start_v as discovered
Q.enqueue(start_v)
while Q is not empty
v = Q.dequeue()
if v is the goal:
return v
for all edges from v to w in G.adjacentEdges(v) do
if w is not labeled as discovered:
label w as discovered
w.parent = v
Q.enqueue(w)
Queue를 이용한 구현
BFS는 일반적으로 큐를 이용하여 구현합니다. FIFO에 따라 먼저 자식 노드들을 일괄적으로 큐에 추가하고 먼저 들어온 같은 깊이의 다른 노드를 Dequeue해서 자식 노드들을 Enqueue할 수 있습니다.
public static int BFS(Graph G, int start_v) {
// let Q be a queue
Queue Q = new LinkedList<Integer>();
// label start_v as discovered
G.visited[start_v] = true;
// Q.enqueue(start_v)
Q.add(start_v);
// while Q is not empty
while (!Q.isEmpty()) {
// v = Q.dequeue()
int v = (int)Q.poll();
System.out.print(v + " ");
// if v is the goal:
if (v == G.getSize())
// return v
return v;
// for all edges from v to w in G.adjacentEdges(v) do
for(int w: G.adjacentEdges(v))
// if w is not labeled as discovered:
if (!G.visited[w]) {
// label w as discovered
G.visited[w] = true;
// w.parent = v
G.parent[w] = v;
// Q.enqueue(w)
Q.add(w);
}
}
// If cannot reach the goal, return 0
return 0;
}
DFS와 동일한 트리에 대해 BFS를 수행해보겠습니다.

public static void main(String[] args) {
int[][] edges = new int[][]{
{1, 2}, {1, 5}, {2, 3},
{3, 7}, {2, 4}, {4, 6},
{6, 8}};
Graph graph = new Graph(8);
graph.addEdge(edges);
Graph.BFS(graph, 1);
}
1 2 5 3 4 7 6 8
총평
DFS와 BFS는 코딩테스트에 단골로 나오는 알고리즘입니다. 처음에는 약간 적응하기 힘들지만 한 번 익숙해지면 매우 간단하게 구현할 수 있습니다. 위 예시에서는 방문 순서대로 노드 번호를 출력하는 간단한 구현을 보여줬지만 실제 문제에서는 동일 구역 찾기, 미로 출구 찾기 등과 같은 응용 문제 형태로 출제됩니다. 의외로 문제풀이만이 아닌 Garbage Collection 복사와 같은 실제 솔루션에서도 유용하게 사용되므로 개발자라면 반드시 숙지하도록 합시다.
위 JAVA 예시 코드는 Github 저장소에서도 찾을 수 있습니다.
Reference
https://en.wikipedia.org/wiki/Depth-first_search
https://en.wikipedia.org/wiki/Breadth-first_search#Bias_towards_nodes_of_high_degree

