스마트폰 시대에 지도 앱이 없는 분은 거의 없을 것입니다.
스마트폰에서 가장 유용하게 쓰는 기능 중 하나입니다. 옛날에는 운전할 때도 글러브 박스에 지도책 하나 넣고 다니는 게 필수이던 시절도 있었습니다.

요즘 지도 어플은 하나의 플랫폼이 되어가고 있습니다.

두 지점의 거리 재기

지도에 있는 기능 중 하나가 두 지점 간 거리를 재는 기능입니다.
차량이나 도보로 이동하는 거리를 측정도 해주지만 측량처럼 두 지점 간의 거리를 재주기도 합니다.

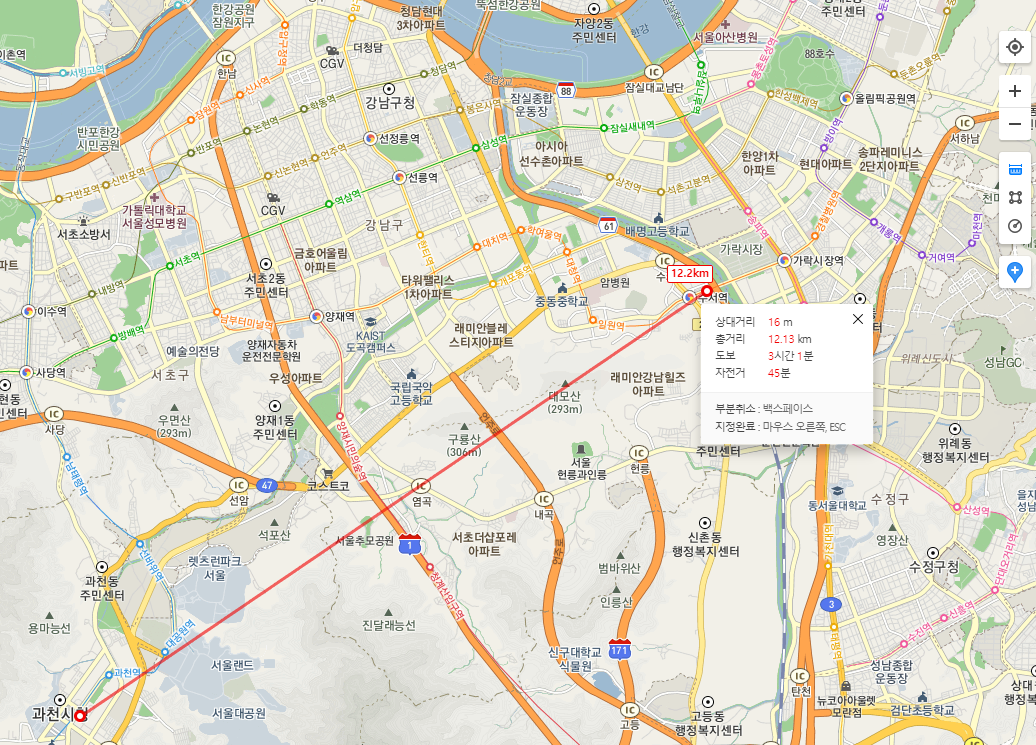
거리를 재는 작업은 매우 중요합니다. 땅 한 뼘에 수십억을 호가하는 명동 땅을 측량 착오로 더 적게 매입한다면 얼마나 손해가 클까요? 따라서 측량기사는 고대부터 매우 중요한 직업으로 인식되었으며 현대에도 자격증으로 검정하는 과목입니다.

요즘은 기술의 발달로 간단하게 터치만으로 두 지점 사이의 거리를 잴 수 있습니다. 두 지점 사이의 위경도 값을 이용하여 계산을 통하여 거리를 잴 수 있습니다. 중고등학교 수학 시간에 두 좌표 사이의 거리를 계산하는 방법을 배웠습니다.

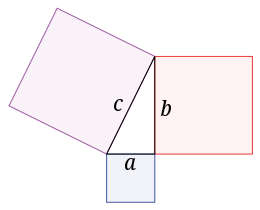
피타고라스의 정리

두 좌표 (x1, y1), (x2, y2)가 있을 때 두 지점 사이의 거리는 x좌표의 차이의 제곱과 y좌표의 차이의 제곱의 합에 대한 제곱근으로 구합니다.

그러나 지구는 둥글기 때문에 위도(Latitude)와 경도(Longitude)로 이런 방법을 써서 구하면 큰 오차가 생기게 됩니다. 매우 짧은 거리야 이런 식으로 계산해도 상관없지만 길이가 길어질수록 지구 곡률의 영향을 받게 됩니다. 두 지표점 사이의 거리는 3차원 공간 상에서 보면 직선이 아닌 호(Arc)의 모양이기 때문입니다. 가장 대표적인 예시로 비행기가 최단 거리로 가는 경로는 2차원 평면 도법 상의 직선거리가 아닌 비스듬한 거리입니다.

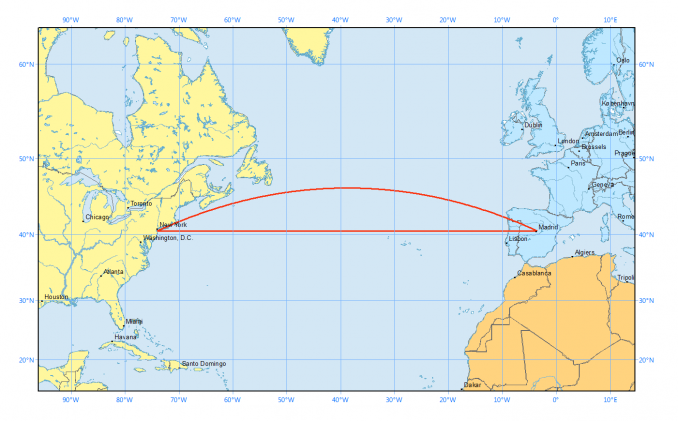
선의 길이는 직선이 더 짧지만 실제 거리는 원호로 표시된 경로가 더 짧습니다.

하버사인 공식 (Haversine Formula)

이런 경우 두 위경도 좌표 사이의 거리를 구할 때 사용하는 것이 하버사인 공식입니다. 공식은 다음과 같습니다.

Θ는 두 점을 잇는 호의 중심각입니다 (라디안 단위)

• φ1, φ2: 1지점과 2지점의 위도 (라디안 단위),
• λ1, λ2: 1지점과 2지점의 경도 (라디안 단위).

hav(Θ)는 하버사인 함수로 다음과 같이 표현됩니다.

거리를 구하기 위해서 역함수인 아크하버사인을 곱해줍니다.

즉, 마지막 공식을 이용하면 두 지점 사이의 거리를 구할 수 있습니다.

코드 구현

한동한 안 쓰던 수학뇌를 갑자기 쓰려면 머리가 아파집니다.
개발자가 수학 공식보다 더 읽기 쉬운 자바 코드로 위 거리공식을 표현하겠습니다.

public static double distanceInKilometerByHaversine(double x1, double y1, double x2, double y2) {
    double distance;
    double radius = 6371; // 지구 반지름(km)
    double toRadian = Math.PI / 180;

    double deltaLatitude = Math.abs(x1 - x2) * toRadian;
    double deltaLongitude = Math.abs(y1 - y2) * toRadian;

    double sinDeltaLat = Math.sin(deltaLatitude / 2);
    double sinDeltaLng = Math.sin(deltaLongitude / 2);
    double squareRoot = Math.sqrt(
        sinDeltaLat * sinDeltaLat +
        Math.cos(x1 * toRadian) * Math.cos(x2 * toRadian) * sinDeltaLng * sinDeltaLng);

    distance = 2 * radius * Math.asin(squareRoot);

    return distance;
}

어느 언어로 구현하나 큰 차이는 없습니다.
그럼 실제로 테스트를 해보겠습니다.

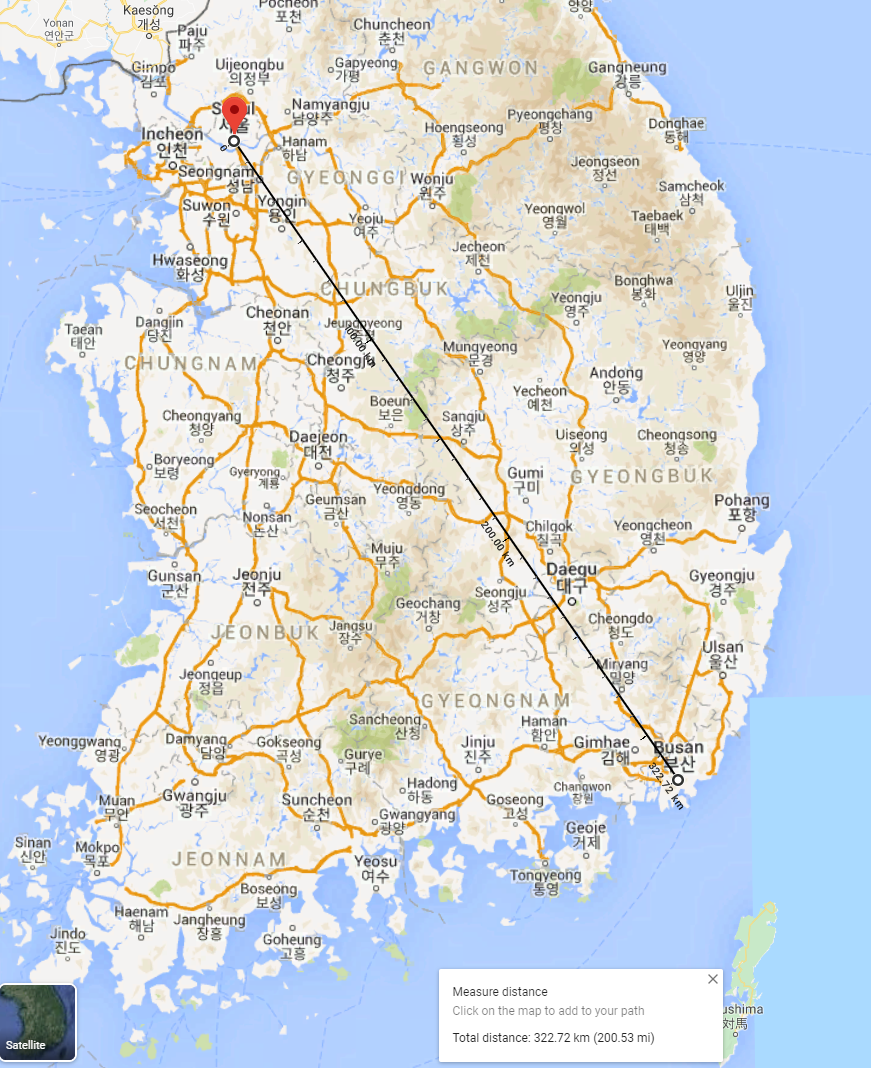
• 서울의 좌표는 위도 37.547889도, 126.997128도
• 부산의 좌표는 위도 35.158874도, 129.043846도

구글맵의 거리재기로 잰 거리는 322.72km가 나왔습니다.

322.72224899963976

자바에서 구현한 공식으로는 322.722km가 나옵니다. 정확한 결과값을 얻을 수 있었습니다. 공식에서는 지구가 완전한 구형이라고 가정을 했지만, 실제 지구는 적도 쪽이 좀 더 길쭉한 타원형이기 때문에 완벽히 정확한 값이라고 할 수는 없습니다. 하지만 일반적인 사용에서는 큰 무리는 없을 정도입니다.

지도 API에서 거리 계산을 해주는 함수가 있지만 좌표값만으로 직접 구해야 할 일이 있을 경우 하버사인 공식을 이용하도록 합시다.

Reference

https://map.kakao.com/
https://www.google.com/maps
https://en.wikipedia.org/wiki/Pythagorean_theorem
https://gisgeography.com/great-circle-geodesic-line-shortest-flight-path/
https://en.wikipedia.org/wiki/Haversine_formula