두 문자열에서 가장 긴 공통 문자열을 찾는 문제는 코딩 테스트의 단골 기출 문제입니다. 영어로 Longest Common Substring Problem이라고 합니다.

Brute force

만약 문자열을 한 자씩 모두 검사한다면, 알고리즘 복잡도는 O(n*2^m)가 될 것입니다. n은 첫 번째 문자열의 길이, m은 두 번째 문자열의 길이입니다.

public String LCSubstr(String s1, String s2) {
    int max = 0;
    int count;
    String ret = "";

    for (int i = 0; i < s1.length(); i++) {
        for (int j = 0; j < s2.length(); j++) {
            count = 0;

            while (s1.charAt(i + count) == s2.charAt(j + count)) {
                count++;
                if (i + count == s1.length() || j + count == s2.length())
                    break;
            }

            if (max < count) {
                max = count;
                ret = s1.substring(i, i + max);
            }
        }
    }

    return ret;
}

Loop 문이 3중첩이기 때문에 짧은 구문의 비교야 금방 끝나겠지만 문자가 길어질수록 속도가 기하급수적으로 느려집니다. 시간 제한이 있는 문제의 경우 거의 틀립니다.

동적 계획법

동적 계획법에 따라 공통 최장 문자열을 구한다면 O(nr)의 복잡도를 갖게 됩니다. 동적 계획법은 한 번 계산했던 결과값을 메모리에 저장하여 계산 속도를 올리는 방법이기 때문에 nm로 공간 복잡도가 늘어납니다.

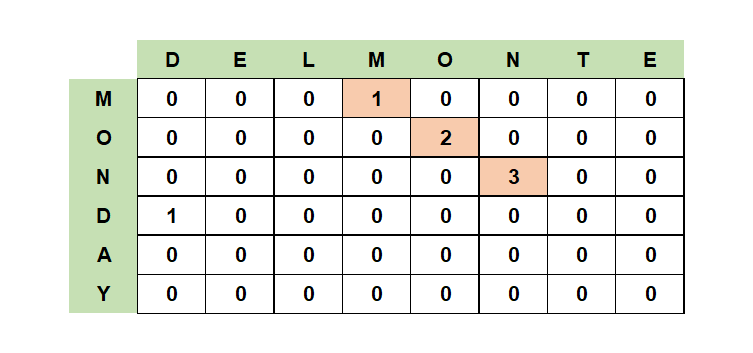
메모용 배열 L의 각 값들은 해당 문자가 몇 번째 연속으로 같은 문자가 나왔는지를 의미합니다. 반복문으로 문자열을 한 글자씩 비교하면서 만약 일치한다면 각각 문자열의 인덱스의 -1에 해당되는 값에 +1을 해줍니다. 위 그림의 빨간 칸을 보면 이해가 쉽습니다. “DELMONTE”를 char 배별로 표현하면 4번 index에 O가 있고 “MONDAY”의 1번 인덱스에 O가 있습니다. 같은 문자이기 때문에 메모용 배열 L의 4,1번째 항목 값에 L의 3,0번째 항목의 값에 +1을 해서 할당합니다.

의사 코드

function LCSubstr(S[1..r], T[1..n])
    L := array(1..r, 1..n)
    z := 0
    ret := {}
    for i := 1..r
        for j := 1..n
            if S[i] == T[j]
                if i == 1 or j == 1
                    L[i,j] := 1
                else
                    L[i,j] := L[i-1,j-1] + 1
                if L[i,j] > z
                    z := L[i,j]
                    ret := {S[i-z+1..z]}
                else
                if L[i,j] == z
                    ret := ret ∪ {S[i-z+1..z]}
            else
                L[i,j] := 0
    return ret

Java 구현

public char[] LCSubstr(char[] S, char[] T) {
    // L := array(1..r, 1..n)
    int[][] L = new int[S.length][T.length];
    // Z := 0;
    int z = 0;
    // ret := {}
    char[] ret = {};

    // for i := 1..r
    for (int i = 0; i < S.length; i++) {
        // for j := 1..n
        for (int j = 0; j < T.length; j++) {
            // if S[i] == T[j]
            if (S[i] == T[j]) {
                // if i == 1 or j == 1, array가 0부터 시작이므로 구현은 0
                if (i == 0 || j == 0)
                    // L[i,j] := 1
                    L[i][j] = 1;
                // else
                else
                    // L[i,j] := L[i-1,j-1] + 1
                    L[i][j] = L[i - 1][j - 1] + 1;
                // if L[i][j] > z
                if (L[i][j] > z) {
                    // z := L[i,j]
                    z = L[i][j];
                    // ret := {S[i-z+1..z]}
                    ret = new char[z];
                    for (int k = 0; k < z; k++)
                        ret[k] = S[i - z + 1 + k];
                }
                // else
                // if L[i,j] == z
                else if (L[i][j] == z) {
                    // ret := ret U {S[i-z+1..z]}
                    ret = new char[z];
                    for (int k = 0; k < z; k++)
                        ret[k] = S[i - z + 1 + k];
                }
            }
            // else
            else
                // L[i,j] := 0
                L[i][j] = 0;
        }
    }

    // return ret
    return ret;
}

다음과 같은 트릭을 이용하여 메모리 사용량을 줄일 수 있습니다.

• 메모이제이션에 사용되는 배열 L을 전체가 아닌 마지막 행과 현재 행만을 메모리에 기억합니다.
• 0이 아닌 값만을 행에 저장합니다. 이 경우 배열이 아닌 해시 테이블을 이용할 수 있습니다. 비교할 길이가 길 경우에 효과적입니다.

Reference

https://en.wikipedia.org/wiki/Longest_common_substring_problem
https://algorithms.tutorialhorizon.com/dynamic-programming-longest-common-substring/